N-Queens Backtracking By Algorithm

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

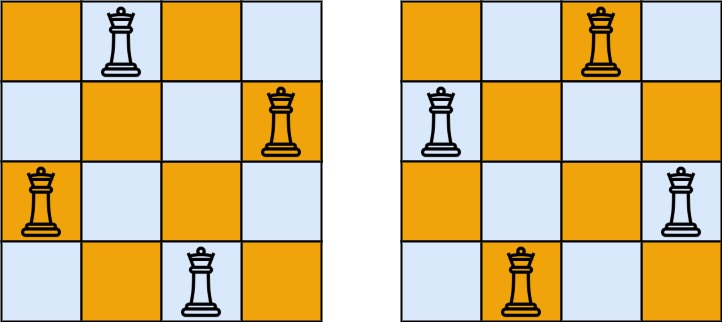
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

JavaScript Solution:

class NQueen {
  constructor (size) {
    this.board = new Array(size).fill('.').map(() => new Array(size).fill('.'))
    this.size = size
    this.solutionCount = 0
  }

  isValid ([row, col]) {
    // function to check if the placement of the queen in the given location is valid

    // checking the left of the current row
    for (let i = 0; i < col; i++) {
      if (this.board[row][i] === 'Q') return false
    }

    // checking the upper left diagonal
    for (let i = row, j = col; i >= 0 && j >= 0; i--, j--) {
      if (this.board[i][j] === 'Q') return false
    }

    // checking the lower left diagonal
    for (let i = row, j = col; j >= 0 && i < this.size; i++, j--) {
      if (this.board[i][j] === 'Q') return false
    }

    return true
  }

  placeQueen (row, col) {
    this.board[row][col] = 'Q'
  }

  removeQueen (row, col) {
    this.board[row][col] = '.'
  }

  solve (col = 0) {
    if (col >= this.size) {
      this.solutionCount++
      return true
    }

    for (let i = 0; i < this.size; i++) {
      if (this.isValid([i, col])) {
        this.placeQueen(i, col)
        this.solve(col + 1)
        this.removeQueen(i, col)
      }
    }

    return false
  }

  printBoard (output = value => console.log(value)) {
    if (!output._isMockFunction) {
      output('\n')
    }
    for (const row of this.board) {
      output(row)
    }
  }
}

export { NQueen }